research

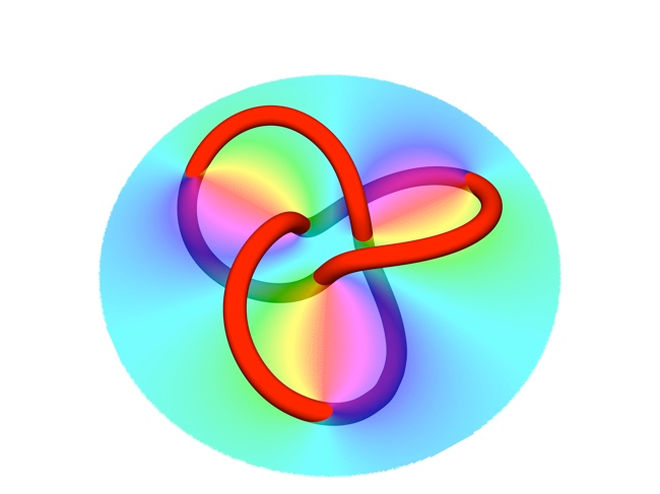
My research is mainly focused on the geometry and topology of fields in physical space, especially in optics, wave physics, and classical field theory. A central theme is understanding how structure, singularity, and topology emerge in real-space configurations — from knotted light fields and the polarisation of sky light to complex molecular and condensed matter textures.

I have contributed extensively to:

• topological, knotted and linked field structures, including optical vortices, topological defects, and knotted field lines in classical electromagnetism
• the theory of singular optics and structured light, especially the geometry of optical vortices and polarization singularities, and momentum flow in wave fields
• geometric phases in classical and quantum systems, with emphasis on nonseparability, optical spin-orbit coupling, and phase topology
• applications of knot theory and applied topology in statistical physics, quantum wavefunctions, and filamentary molecules
• broader themes in mathematical physics, including symmetry, field theory, quantum chaos, and the visual and topological aspects of Fourier and real-space representations of waves and fields

Much of my recent work draws on or feeds into topological design — using mathematical insight into field structure to guide future experimental and technological systems.

I collaborate widely with other theorists and also experimental optics and condensed matter groups worldwide.